Eikonal Optics offers various photodetector modules including a transimpedance amplifier equipped with a conventional photodiode and a biased/amplified silicon photomultiplier (SiPM).
The quantum efficiency curve of a SiPM is distinct from that of common photodiodes (see the blue curve in Fig. 1). Appendix A summarizes key topics about the detection process including quantum efficiency, the photoelectric effect, photoconduction in an intrinsic semiconductor, and photodetection in the PN junction of a semiconductor diode.

The SiPM is an array of Si photodiodes operated at sufficiently high reverse bias that electron-hole pairs created by absorption of a single photon triggers a charge avalanche, which results in a gain of \(\sim 10^6\). As a consequence, the SiPM is sensitive to individual photons.
The ability to detect individual photons by itself does not guarantee high sensitivity. Signal-to-noise ratio is an important figure of merit for a detector and quantum efficiency is a key factor in determining the strength of the signal. The quantum efficiency of a conventional photodiode is the probability that an incident photon creates an electron-hole pair that contributes to the photocurrent. The quantum efficiency of a SiPM is the probability that an incident photon produces an electron-hole pair that results in a charge avalanche.
Quantum Efficiency of Photodiodes
Three basic factors prevent a photodiode from achieving a broad wavelength sensitivity: 1) silicon has a high refractive index; 2) at long wavelengths near the absorption cutoff (1100 nm) the absorption length becomes very long; and 3) at short wavelengths (< 400 nm) photons are absorbed within a very shallow layer.
The high index of refraction of silicon (\(n\) = 4.0 at 580 nm) means that Frensel reflection losses (36% at 580 nm) are high and an anti-reflection (AR) coating is necessary to achieve good efficiency. High temperature oxidation of Si in an oxygen atmosphere to SiO\(_2\) (\(n\) = 1.47 at 580nm) conveniently forms a thin dielectric layer that reduces the reflectivity and improves the photodiode quantum efficiency without the need to add additional exotic materials. If higher performance is needed, materials with a better index match for a \(\lambda/4\) coating exist, e.g., HfO\(_2\) with or indium tin oxide (ITO). Both have \(n\) = 1.90 at 580 nm.
At wavelengths approaching 1100 nm silicon effectively becomes transparent and a very thick (few 100 \(\mu\)m) depletion region is required so that photo-generated charge carriers are efficiently collected and contribute to the measured photocurrent. Red sensitive detectors can be fabricated using high-resistivity silicon, which allows the formation of depletion region depths of several hundred microns.
Conversely, at short wavelengths the absorption length is small (10 nm at a wavelength of 400 nm) and photo-generated electron-hole pairs may recombine in surface layers before they reach the depletion region.
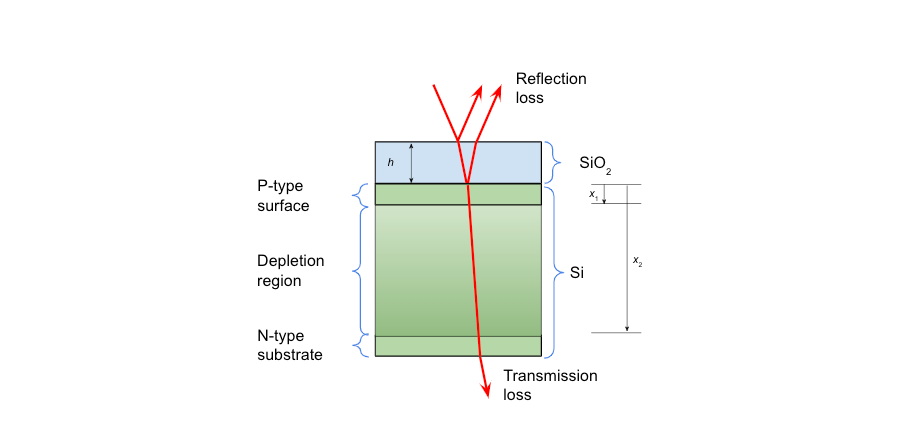
We adopt a model for quantum efficiency that describes the photodiode detector as a three layer structure: 1) a dielectric surface layer of SiO\(_2\) that acts as an anti-reflection coating; 2) a thin passive surface layer of Si where photocarriers recombine or otherwise are lost to the measured photocurrent; and 3) a second active layer of Si where photocarriers are collected with 100% efficiency. This model implies that the differences between the curves seen in Fig. 1 can be accounted for by adjusting the three thickness parameters: \( h\), \(x_1\), and \(x_2\) shown in Figure 2.

Modeling Photodiode Quantum Efficiency
Figure 3 shows the quantum efficiency curve for a Vishay BPW20RF, which is a readily available planar silicon PN photodiode.

The solid line in Figure 3 shows the best fit model for a Vishay BPW20RF photodiode indicating that this simple three-parameter description captures measured characteristics of this device. Three different variants of the model are shown as various broken lines. The dashed line shows the reduction of efficiency if the SiO\(_2\) layer is omitted. The omission of the SiO\(_2\) AR coating reduces the overall efficiency by about 20%. The dotted line represents a variant of the best fit model where all photocarriers created near the top of the device contribute to the photocurrent—removal of the surface recombination zone improves the response at 400 nm by more than a factor of 2. The dot-dash line shows the potential increase in efficiency at long wavelengths for a very thick device.
A second example is shown in Figure 4, which features a Marktech MT03-002. This is a photodiode with enhanced blue sensitivity. A version of our TIA-F-01 transimpedance amplifier is available equipped with this blue/green optimized diode.

Silicon Photomultiplier
Figure 1 shows that the quantum efficiency curve of the onsemi MICRO-FC-30035 SiPM is distinct from that of conventional photodiodes. A model fit to the SiPM quantum efficiency in Figure 5 explains the distinctive features of the quantum efficiency curve are due to the properties of the depletion layer. The blue sensitivity is associated with a depletion layer that is very close (2 nm) to the surface (similar to the blue-green optimized Marktech MT03-002 diode in Fig. 4). The low efficiency at long wavelengths is due to the thinness of the depletion layer (1.2 \(\mu\)m) so that this device is effectively transparent in the red. This model also includes a wavelength independent correction for the SiPM microcell area filling factor, \(\mathcal{F}\) in Eq. (B1).
The fit in Figure 5 overestimates the efficiency at wavelengths shorter than 350 nm. Onsemi SiPMs are encapsulated using a clear transfer molding compound, which is not included in the model. Strong absorption shortward of 350 nm is typical of optical-grade epoxies and the UV quantum efficiency deficiency relative to the best fit may be caused by absorption in this layer.

| Detector | Max QE/ Wavelength | AR Coating thickness | Depletion layer depth | Depletion layer thickness | |
|---|---|---|---|---|---|
| \( h \ [ \mu \rm{m} ]\) | \( x_1 \ [ \rm{nm} ]\) | \( x_2 \ [ \mu \rm{m} ]\) | |||
| BPW20RF | 0.92 @ 780 nm | 128 | 76 | 267 | |
| MT03-002 | 0.88 @ 560 nm | 88 | 3 | 244 | |
| MICRO-FC-30035 | 0.40 @ 430 nm | 55 | 2 | 1.2 |
Appendix A: The Photoelectric Effect, Photoconductors, and Photodiodes
The photoelectric effect in its original form (also known as the photoemissive effect), employs a metallic electrode in a vacuum tube (Fig. A1). One electrode is illuminated, and the absorption of a photon ejects an electron from the surface, which is collected by a second electrode to yield a photocurrent, \[ I_{ph} = \eta \; \mathcal{G} P \frac{q_e }{h\nu} . \tag{A1}\] Here, \(\eta\) is the quantum efficiency or the fraction of incident photons absorbed, \(\mathcal{G}\) is the gain, \( P \) is the incident radiant power at frequency \(\nu\), \(q_e\) is the fundamental charge, and \(h\) is Planck's constant. In a photomultiplier, an electron avalanche leads to \(\mathcal{G} \gg 1\).

The photoelectric effect in a semiconductor is the basis of a device known as a photoconductor. An intrinsic semiconductor, such as pure Si, CdS, or PbS is used, unless far-infrared response is required. The detector is completed by applying ohmic contacts to the semiconductor so that the resistivity can be measured as shown in Fig. A2.
The conduction band of an intrinsic semiconductor is virtually empty in the absence of illumination and the resisitivity is correspondingly high. The absorption of a photon in the bulk material (there is no PN junction in this type of detector) generates an electron-hole pair and hence a photocurrent also described by Eq. (A1).

A photoconductor is always operated at non-zero bias voltage, so the electric field within the device tends to separate the photogenerated electrons and holes so that they can be collected by the electrical contacts and the photocurrent measured.
Electron-hole recombination can remove photocarriers before they are collected by the electrodes and \(\mathcal{G}\) can be less than unity. Conversely, if the time for carriers to cross the device is substantially shorter than the recombination time, \(\mathcal{G}\) can be larger than unity. If a photoelectron reaches the the positive electrode then by charge neutrality a replacement electron must be injected at the opposite contact. Thus any given photoelectron may circulate multiple times if the recombination time is long. The same is true for holes.
Although the photoconductive effect just described seems an effective basis for detection of light, there are several limiting factors including non-linearity, excess noise, and reduced signal bandwidth. These are avoided if photodetection occurs within the depletion region of a PN junction. This is the case for photodiodes and SiPMs.
At the interface between the P and N sides of a unbiased PN junction the majority carriers from each side diffuse across the boundary. Electrons recombine with holes, forming a region depleted of carriers. The parent donor and acceptor ions are locked within the crystal lattice and are immobile. This means that any photogenerated electron hole pairs created in the depletion region are separated by an intense electric field. Recombination is effectively rendered irrelevant. Therefore, \(\mathcal{G}=1\) in a PN photodiode as photogenerated electrons and holes are separated and then moved to the region where they are the majority carrier.
A solid state silicon photomultiplier (SiPM) is an array of photodiodes with gain due to the avalanche effect. The number of photodiodes (or microcells) affects the linearity of the device. Making an efficient SiPM, or any photodiode, involves getting the light into the depletion region and making sure that the light is absorbed there.
Appendix B: Quantum efficiency, Absorption of Light, and the Complex Index of Refraction
To compute the quantum efficiency of a detector we adopt a 1-d model defined by the thickness and composition of various plane layers sketched in Figure 2. The structure consists of a top dielectric layer of SiO\(_2\), which acts as an antireflection coating, followed by an inert layer of Si followed by the depletion region. We assume that all the photocarriers generated by the absorption of photons in the depletion region comprise the photocurrent (photoconductive gain \(\mathcal{G} = 1\)). Photons that propagate all the way through this active region escape detection and are lost out the back of the device.
We use a classical description of the propagation of an electromagnetic (EM) wave in a stratified medium. We compute the reflection and transmission coefficients at the various interfaces at the surface and within the device, and then use the complex part of the index to find the absorption within each layer of the photodiode.
If the quantum efficiency, \(\eta_\lambda\), is the fraction of photons at a given wavelength that contribute to the photocurrent then, \[ \eta_\lambda = \mathcal{F} \; [1-R_\lambda ] A_\lambda (x_1,x_2) , \tag{B1} \] where \(R_\lambda\) is the fraction of incident light lost to reflection at the surface and \(A_\lambda(x_1,x_2)\) the fraction that is absorbed internally in the depletion region located between depths \(x_1\) and \(x_2\). When computing \(R_\lambda \) we assume normal incidence so that polarization can be neglected, and \(R_\lambda\) only depends on the index of refraction, \(n\), which in turn depends on wavelength. The factor, \( \mathcal{F} \), is included to describe the SiPM microcell filling factor. \(\mathcal{F}\) varies with microcell dimensions: 28% for 10 \(\mu\)m cells; 48% for 20 \(\mu\)m cells; 64% for 35 \(\mu\)m cells; and 72% for 50 \(\mu\)m cells.
Index of Refraction and Absorption
A linearly polarized beam of light at frequency, \(\nu = \omega/(2\pi) \) or vacuum wavelength \( \lambda_0 =c/\nu\), propagating in the \(x\)-direction is represented by a plane EM wave with electric field described by \[ E = E_0 \exp{[\mathbb{i}( k x -\omega t)]}. \tag{B2}\] The wavenumber, \(k\), is given by the dispersion relation, \( k = \omega n /c\), where \(c\) is the speed of light in vacuum (\(n=1\)). For a pure dielectric material, \(n\) is real and the exponent describes undamped oscillatory behavior.
If \(n\) is complex, with \(n = m + \mathbb{i} \kappa \), the spatial part of Eq. (B2) now includes an exponential decay varying as \( \exp{(-2 \pi \kappa x /\lambda_0)} \), which describes the amplitude of the electric field diminishing with distance propagated.
The intensity of a beam of light is proportional to amplitude of the electric field squared; hence, the attenuation of the beam in the presence of absorption is governed by \[ I = I_0 \exp{(-4 \pi \kappa x /\lambda_0)} . \tag{B3}\]
The absorption coefficient is \( \alpha = 4 \pi \kappa /\lambda_0\) and the fraction of incident light absorbed in a slab between depths \(x_1\) and \(x_2\) is therefore \[ A_\lambda(x_1,x_2) = \exp{(-\alpha x_1 )} - \exp {(-\alpha x_2 )} . \tag{B4}\]
Measurements of \(m\) and \(\kappa \) versus wavelength are available for a broad range of materials including silicon.